電気計測の基礎(1)
電気計測の基礎 (1)
1.電気計測 基礎編
目 次
(紫色の部分をクリックすると、その項目に移動。戻るときはブラウザの←をクリック)
・アナログとデジタル
・電気計測で測るのは、直流電圧
・AD変換
・ビットと精度(正確さ)
・比較測定か絶対測定か
・確かめる必要性・・信頼性
・すべてを直流電圧に変換する
・・電流を電圧に変える方法
・・抵抗を電圧に変える方法
――――――――――――――――――――――――――――――――
電気計測は、「装置を作る」のに必要な一部分です。
装置には、
・環境条件をつくること(たとえば、試料の温度を一定にする、圧を一定にするなど)、
・状況を測ること(例えば、温度や圧力はどれだけか、どれだけエネルギーや物質が流れたか、など)があります。
電気計測はこの両者に関わります。
電気計測は文字どおり「測る」ことがメインですが、環境条件である温度や圧力などをコントロールするのにも必要です。制御しつつ測る作業に欠かせません。
このHPで、電気計測の全てを記載することはなかなか大変です。というより、私たちの手に負えません。しかし、私たちはいろいろ電気計測のお世話になってきました。そこで、私たちが手掛けた部分(かなり初歩的な)をご紹介して、少しでもお役に立てればと思います。
初めて電気計測を始めようとするかたが対象です。詳しくは、たくさん出ている専門書を参考にしてください。いわば、専門書への導入編です。
・アナログとデジタル
アナログは連続量をいいます。デジタルは離散的な量をいいます。時計で針が動くアナログ時計とデジタル時計はいい例でしょう。電気計測ではこの両者を扱います。実際はアナログ量ですが、それをデジタルに変えて扱うことが大部分です。
電気については、直流と交流がありますが、電気計測で扱うのは大部分が直流です。液体の電気抵抗を測る時など交流を使いますが、最終的には直流に変換します。
直流はとても簡単なオームの法則で表されます。
I=V/R または V=IR
はよく知っています。
ついでですが、オームの法則は、土壌物理で扱う、水、ガス、熱の流れと全く同じ形式 [流束=透過係数・ポテンシャル勾配]で表されます。
余談になりますが、これは、ある計測器メーカーで研究開発をされている方の話ですが、電気の専門家と言われる人でも「オームの法則を理解している人は少ない」というのです。皆さんはもちろん、「いや、V=IRくらい知っている」、と答えるでしょう。でも、「回路をみて、ここにはこのくらいの電圧、あるいはこれだけの電流が流れていると分かる人は少ない」、というのです。つまり、どこに、どれだけの電気が流れているのを理解して、初めて、「オームの法則が理解できた」と言えるというのです。
これを聞いて、思わず、自分のことを考えてしまいました。これは電気だけでなく、水であれ、ガスであれ、熱であれ、すべて流れを扱うことに通じます。「自分は本当に流れを理解できているのだろうか?」と。
皆さんはいかがですか?
いまこの装置で、あるいは、この地点でこれ位の流量がある、ここにこれ位のヘッドロスがある、・・・・。
土壌物理を対象とするみなさんは、ぜひ、「流れが読める」ようになっていただきたいと思ってあえてこの話をご紹介した次第です。
とても大事なことがあります。それは、電気計測で測るのは、「直流電圧だけ」、ということです。
交流の場合は、直流に変換しなければなりません。
抵抗も電流もすべて、電圧に変換して測ります。
最近のセンサーはAD変換を考慮して、出力を電圧や電流にしてあるものになっています。
たとえば、湿度計ですが、中に相対湿度を測定する回路を組み込んでいて、出力が0-1Vで相対湿度が0-100%に対応しているものが販売されています(例:TDK CHS-Uタイプなど)。
・AD変換
AD変換のAはアナログ、Dはデジタルの略です。アナログ量をディジタル量に変換する場合、実際にどうやって行うのか、という話です。
それには、AD変換器を使います。
AD変換器ではここに入れるアナログ入力の範囲が決められています。たとえば、0~1V、0~10mVという具合です。そして最大の電圧をフルスケール(FS)と言います。
下の図を見てください。このフルスケールのアナログ電圧を3ビットのAD変換器を通すとどうなるか、を示します。
3ビットは23、すなわち8です。FSを8分割し、2進数(括弧内は10進数)でいえば、000(0)、001(1)、010(2)、011(3)、100(4)、101(5)、110(6)、111(7) となります。
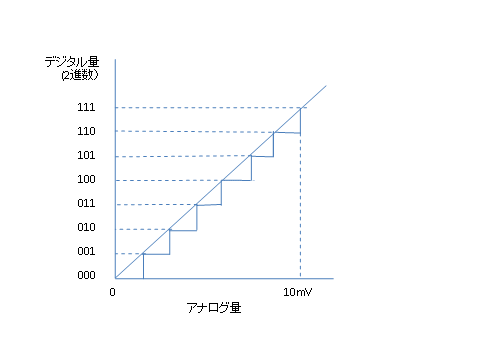
AD変換の原理は、変換器の内部にある基準電圧と入力された電圧とを比較します。詳細は専門書を見ていただくとして、たとえば、以下のようにAD変換をします。
・パルスを発生させ、パルスをカウントすると同時にカウント数に見合う電圧を発生させます。
・この電圧と入力電圧と比較し、等しくなったときのパルスの数をデジタル出力とします。
実際の測定では8ビット(256)、12ビット(4096)、16ビット(65536)などが用いられます。ちなみに12ビットでFSが10mVだと、ビットサイズ(最小単位)は0.0000025Vとなり、2.5μVが最小計測量となります。
私たちがかつて使っていた装置にグリーンキット88がありました。まだ、どこかの研究室の片隅にあるかも知れません。この装置のAD変換器は入力は10mV FSで 12ビットでした。とても安定した、使いやすい装置でした。
銅・コンスタンタン(CC)の熱電対は1℃あたり40μVの出力があるので、0.0625℃の精度で測れることになります。
ここで、関連して、ビット数と精度(正確さ)について考えてみましょう。
ビット数が多ければ正確か?
カメラのピクセル数と同じで、ピクセル数が多いからといって必ずしもきれい(正確)に写るわけではありません。逆にピクセル数がそれほど多くなくても、きれいに写るカメラがあります。これはレンズの解像度がいいから(入力の品質が良いから)です。
というわけで、AD変換のビット数(桁数)が大きいから精度が高いとは必ずしも言えないのです。ビット数が多いほど感度は高くなります。しかし、感度が高ければ正確さが増すことと同じではありません。まず、アナログ入力自体が正確で安定していなければなりません。
温度測定の場合を考えてみましょう。
センサーを銅・コンスタンタン(CC)熱電対を使い、精度を0.1℃まで測ろうとします(熱電対の使い方については、別のところで説明します)。1℃あたり、約40μVの起電力があるので、0.1℃は4μVに相当します。
先ほどのFS10mVで12ビットのAD変換器は最少で2.5μVまで測れるので、これで可能となります。
しかし、FSが10mVで0.1μVまで測りたいとすると、12ビットのAD変換では間に合いません。16ビットで最少が0.15μV。これでも少し荒すぎます。18ビット(最少単位が0.04μV)の分解能はほしいところです。
このように、精度を考え、ビット数も決める必要があります。もちろん計算上は12ビットのAD変換器を通しても、20.001℃などという表示(数字)は出せます。でもその値に意味はありません。
・比較測定か絶対測定か
測定には絶対測定と比較測定があります。
どちらが良いかは、ケースバイケースですが、一般的には、相対測定が有利です。
絶対測定は測ろうとする物理量の次元のそれぞれを測り、得られます。たとえば、熱伝導率は、[J /(s m K)]なので、4つの次元について測ることになります。これは、正直、大変です。
相対測定はたとえば水の物性値を基準に別の物質の物性値を測るといった方法です。
こちらの方が、断然有利です。なぜなら、次元どおりの測定ではそれぞれの次元ごとに誤差が入りこむ可能性があるなかで、比較して測れば、これらの誤差を避ける(相殺できる)ことができるからです。
このように、相対測定ができる場合は、そちらを選ぶのが有利です。
正確なデータを得ることができれば、そのデータのもつ精度の限界まで解析することができます。
正確な測定とは、なにより、同じものを測ったとき、同じ値が得られること、すなわち、繰り返し精度のよいことです。
私は、あくまでも正確なデータを取るということが、実験物理の根幹にあると考えています。外乱の多い環境で、多数回の計測を行い、それを統計処理して正しい値だと評価する(推測する)という方法は取りませんでした。(そういう方法があるということは十分認めています。)
もう1つお話ししなければならないことがあります。
それは、すべての計測にも言えることですが、電気計測で得られた値は信頼できるかという問題です。
とくにコンピュータとつながった電気計測では、得られた結果が、何桁も表示できます。すぐに表計算ソフトにデータを取り込み、処理できます。
いきおい、「これは正確なデータにちがいない」と思ってしまいがちです。
それが大きな落とし穴になる場合があります。
私は、そこに、「確かめる」という操作が必要だと考えています。たとえば、別の測定器で測ったデータと、そのデータが一致するかを調べるということです。温度なら、標準温度計で校正した温度計を用いて、データが一致するか、電圧測定なら別のデジボルで測ったデータと一致するか、などを確かめることです。
「確かめる」という操作なしに得られた結果は、「データとして使わない」ことです。
私はこの過程は必須だと考えています。
逆に、確かめておけば、計測データとして安心して扱える、ということになります。
くどいようですが、「確かめる、という操作を最低一度(できたら度々)行うこと」。これは、電気計測の場合に限りませんが、とくに電気計測では鉄則です。
・・直流電圧のフルスケールを調整する
電圧も先に書いたように、ある範囲内に収めねばなりません。たとえば5Vが最大というときに、1Vがフルスケールではオーバーしてしまいます。その時は、最高電圧を落とさねばなりません。
簡単な方法は、抵抗分割を行います。
回路の抵抗がR2の場合、回路に図のように電気抵抗R1を入れます。するとR1の両端の電圧は、
V1=V R1/(R1+R2)
となります。R1を適当に選べば、測りたいFSまで電圧を低下できます。なお、抵抗は温度依存性の小さい金属皮膜抵抗を使います。
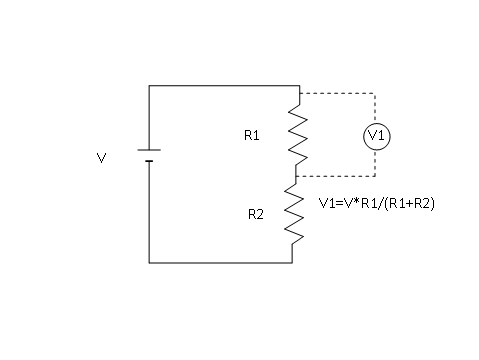
抵抗値が大きいと、電流はあまり流れないので電力も消費しません。
正確な比にするために、調整のための抵抗を入れれば可能です(図)。こんなとき、精度のいいデジボルがあると重宝します。
電圧が小さいとき大きくするには、増幅を行います。
増幅は、かつてはメカニカルチョッパーと言って、機械的に直流を交流に変えて増幅する方法を使いましたが、現在はオペアンプで精度よく増幅することができます。
・・電流を電圧に変える方法
オームの法則を思い出してください。
I=V/R あるいは V=I R
です。
すなわち、回路に抵抗を入れてその両端の電圧を測ることで、電流量が測れます。
抵抗は温度によって抵抗値が変化しない金属皮膜抵抗を使います。
電流を測る必要があるのは、長い距離をケーブルで送信する場合、ケーブルの電気抵抗で電圧が下がってしまうと正確な測定ができません。この場合、電流で送ると正確に送れます。理由は、オームの法則を思い出してください。
・・抵抗を電圧に変える方法
抵抗が変化する場合にその抵抗を電圧に変える場合がほとんどです。
この場合、ブリッジ回路を使います。下図はその1例です。
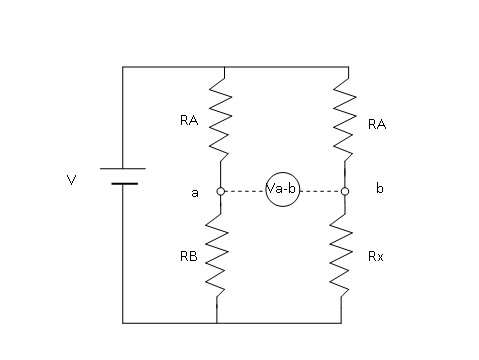
2つの直列抵抗の両端に定電圧Vをかけます(定電圧電源については別のところで説明します)。
2つの直列抵抗の間の電圧を測ります。左側の直列抵抗は、温度などにより抵抗が変化しない抵抗体(金属皮膜抵抗など)、右側のAは左側と同じく抵抗が変化しないものを用い、Xに測りたい抵抗を入れます。そして、a、bの2点間の電圧を測ります。
Xの抵抗RXがRBと同じだと、a-b間の電圧はゼロです。もし、RXが大きくなると、右側の抵抗に流れる電流は、V/(RA+RX)となり左側の電流
V/(RA+RB)より小さくなります。すると左側a点の電圧をゼロとすると、b点の電圧はRX*V/(RA+RX)となりa点の電圧RB*V/(RA+RB)より大きくなり、A<<Bという条件では、
(RX-RB)*V/(RA+RB)
にほぼ等しくなり、a-b間の電圧はXの変化量に比例するとみなせます。
この方法は、抵抗温度計やサーミスタ温度計を用いるときに利用します。