塩類集積のメカニズム
塩類集積のメカニズム
塩類集積のメカニズム
塩類集積には,(a) 灌漑を行うことにより土層に含まれている塩が地表付近に集積して作物生育に障害を与える場合と,(b) 灌漑水に含まれる塩が根群域の塩濃度を上昇させて(この場合は根群下端の塩濃度が最大となる)作物生育に障害を与える場合とがある。さらには,(a)と(b)との相乗作用により塩類集積が生じる場合もあるだろう。
ここでは,(a)の場合の塩類集積のメカニズムを解説する。灌漑農業が必須の乾燥地,半乾燥地では,自然状態では塩は地表ではなく下層に存在するという。その理由は土壌生成過程のことでありここでは触れない。そして良くいわれているのは,灌漑により地下水位が地表から2~3 mよりも浅くなると塩類集積が生じるということである。そこで出てくる最初の疑問は,地下水面が上昇したのは,灌漑水量が蒸発散量を上回ったためであり,土中に含まれる塩は下降こそすれ,上昇はしないはずであるということである。実際,鉛直カラムの一部に塩濃度の高い層を作って土を均一に充塡したとき,灌水量が土面蒸発量を上回れば,塩濃度の高い層は下方へ移動する。したがって,農地で塩類集積が発生するかどうかは灌水量と蒸発散量の収支では理解できず,流れる水の形態を考えなくてはならない。
土中の水移動は大きく分けて飽和流と不飽和流とがある。飽和流とは湛水する条件下の水移動で生じる。この場合,水は土を構成するマトリックス(基質)の孔隙を流れるのに加え,マトリックスを貫通する粗孔隙があれば,粗孔隙を集中して流れる。これをバイパス流(マトリックスを迂回する流れ,preferential flowともいう)という。土を充塡したカラム試験のような場合には水移動はマトリックス流であるが,粗孔隙の発達した構造土(structured soil)の水移動はバイパス流の寄与が非常に大きい。一方,不飽和流は土面蒸発の際に土中で生じている上向きの水移動や,しとしと雨やドリップ灌漑のように地表面に水たまりができない程度の,降雨(散水)強度が小さい条件下で生じる。粗孔隙は飽和から不飽和になるとき,最初に水がなくなるので,不飽和ではバイパス流は存在せず,マトリックス流となる。飽和と不飽和,マトリックス流とバイパス流といった流れの形態が塩類集積に大きく関与する。
塩類集積が生じている農地の特徴として,(1)粗孔隙の発達した土である場合と,(2)細粒土と粗粒土がパッチ状に分布する場合とがある。そこで,両者の塩類集積のメカニズムを考える。
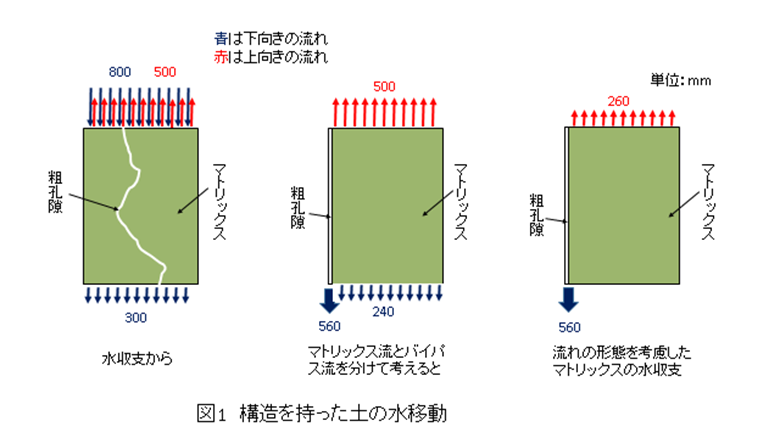
1. 粗孔隙が発達した農地
図1のように,土層のマトリックスを貫通する粗孔隙がある場合,ボーダー灌漑やベイスン灌漑のように地表が湛水する条件下では,土層を浸透する水の大半は粗孔隙を優先的に流下するバイパス流である。バイパス流は土のマトリックスと触れあうことが少ないため,土層に含まれる塩を殆ど溶かさずに,ほぼ灌漑水の塩濃度で土層を流下する。一方,蒸発散に伴う上向きの水移動の場合は,水移動は不飽和状態で生じるマトリックス流である。溶質はマトリックスの孔隙内に存在するので,マトリックス流の溶質濃度はマトリックスの溶質濃度に近くなる。例えば,年間の灌漑水量が800 mm,蒸発散量が500 mmあり,灌漑水量の7割がバイパス流で土層を流下すると仮定する。なお,マトリックス流の寄与(この例では3割)は洗脱効果係数に相当する(Bolt & Bruggenwert, 岩田他訳,土壌の化学,第9章)。マトリックスを下向きに流れる水量は240 mmなのに対し,マトリックスを上向きに流れる水量は蒸発散量に等しい500 mmである。この結果から,灌漑水量と蒸発散量の差,300 mmは毎年,地下水を上昇させる一方,マトリックス流による水移動は差し引き260 mmの上向きの流れであり,土層中の塩を地表に向かって運ぶ。構造土ではこのようにして地表面に塩が集積する。
2. 細粒土と粗粒土がパッチ状に分布する農地
1枚の灌漑区(ボーダー灌漑では畦に囲まれた区画)に粗粒土と細粒土が水平方向に分布する畑では,粗粒土の役割は構造土の粗孔隙と類似している。粗粒土では飽和透水係数が大きいので浸透水量が多く除塩が行われる可能性が高い。一方,蒸発散に伴う上向きの水移動量は細粒土の方が大きくなる可能性がある。その結果,粗粒土では除塩が細粒土では塩類集積が起こることになる。言葉で表現すると,このようになるが,畑面積の割合と飽和透水係数の違いに着目して塩類集積を考えてみる。
農地が均質な場合,湛水条件下の下向きの浸透は,下向きの流れを正としたとき,次のダルシーの法則により表される。
Q/(A t)=k (d+l-p)/l (1)
ここでQは灌漑水量(m3),Aは農地面積(m2),tは浸透時間(s)である,kは飽和透水係数(m/s),dは湛水深(m),lは土層の長さ(m),pは土層下端の水圧(m)である。この式にはd, l, pが含まれているが,湛水深が浅く,土層の厚さが長く,なおかつ土層下端の水圧がゼロ(大気圧に等しい)と仮定すると,(1)式の右辺は近似的に透水係数に等しくなる。この仮定は,飽和土中の水は重力のみによって下に流れているということである。灌漑水量を雨と同様に水深h (m)で表すと,Q=Ahと(1)式からh=ktという関係が得られる。また,灌漑水量は土中を流れた浸透水量に等しい。
つぎに,面積Aの農地が図3のように面積A1の細粒土畑と面積A2の粗粒土畑に分けられる場合を考える。そして,細粒土畑と粗粒土畑の浸透水量がh1, h2,飽和透水係数がk1,k2の場合,
畑全体の灌漑水量は h=kt
細粒土畑の浸透水量 h1=k1t
粗粒土畑の浸透水量 h2=k2t
となる。ここで,kは農地全体の平均透水係数ということになる。
一方,各畑の浸透水量の和は畑全体の灌漑水量に等しいので,
Ah=A1 k1 t+A2 k2 t (2)
細粒土畑面積の割合をr (0<r<1),k2/k1= α (α>1)とおいて(2)式を変形すると,
h=k1 t(r+α(1-r))
したがって,細粒土畑の浸透水量h1と粗粒土畑の浸透水量h2はそれぞれ次のようになる。
h1=h/(r+α(1-r) ) , h2=αh/(r+α(1-r) ) (3)
灌漑のたびに(3)式に相当する浸透が生じているとすると,年間を対象にしたときはhを年間の灌漑水量にしても(3)式は成り立つ。
灌漑に伴う下向きの浸透に対して上向きの蒸発散は次のように考える。上向きの水移動はもっぱらマトリックスを通して行われる。そして,土面蒸発で土が乾燥していく過程では駆動力としてマトリックポテンシャル勾配が卓越するので,不飽和水移動を表すバッキンガム・ダルシー式は(4)式のように表される。
Ju=-k(ϕ) Δϕ/Δz (4)
ここでJuは上向きの流束(ある水平断面を単位時間に上向きに通過した液状水の体積を断面積で除した値で速度と同じm/sの次元を持つ)であり,上向きの流れを正とする。k(ϕ)は不飽和透水係数(m/s)でマトリックポテンシャルϕ (負の値)の函数であることを示す。zは鉛直方向の距離で,Δϕ/Δzはマトリックポテンシャル勾配(無次元)を示す。
土が乾燥(マトリックポテンシャルの負の値がより大きくなる)するにつれ,不飽和透水係数は低下する。その特徴は図2に模式的に示すように,粗粒な土ほど大きく,細粒の土では小さい。
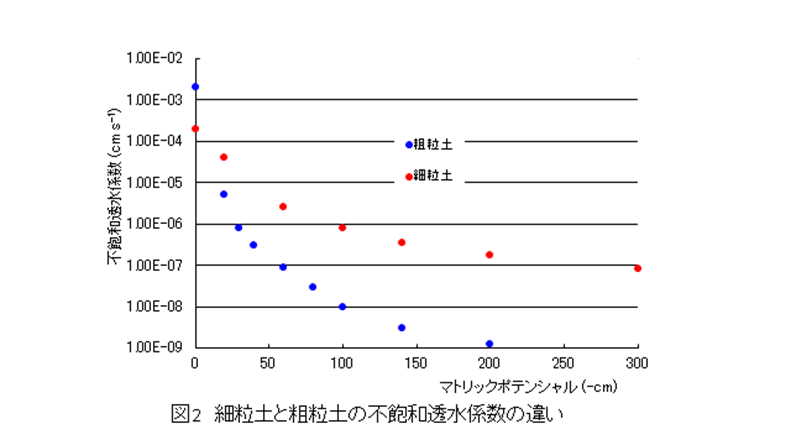
湿った土が土面蒸発により乾燥していく過程を観察すると,乾燥に伴い透水係数は低下し,マトリックポテンシャル勾配は増加することで,短期的にはJuは一定に保たれるが,さらに乾燥が続くとk(ϕ)の低下をΔϕ/Δzの増加で補えなくなり,蒸発速度は低下していく。したがって,粗粒な土では蒸発は早期に非常に小さくなり土面蒸発量が少ないのに対し,細粒な土では粗粒土よりも蒸発速度は大きくより長期に続くことになる。
以上のように,除塩に寄与する灌漑に伴う下向きの水移動と塩類集積をまねく土面蒸発に伴う上向きの水移動を説明してきたが,適当な数値を入れてパッチ状畑の水移動を直感的に理解してみよう。灌漑水量が900 mm,蒸発散量が540 mmで細粒土畑が全体の1/3を占め,粗粒土の飽和透水係数が細粒土のそれの4倍とする。上向きの水移動については,粗粒土の水移動量を過大に評価するように細粒土も粗粒土も上向きの水移動量は蒸発散量に等しいと仮定する。以上の条件で下向きの浸透量を計算すると,細粒土では300 mm,粗粒土では1200 mmとなる。一方,蒸発散に伴う上昇流は両者とも540 mmであるので,正味の水移動は細粒土では上向きに240 mmとなって塩類集積が生じる条件となるのに対し,粗粒土では下向きに660 mmと土層内に含まれる塩が除塩されることになる。以上の様子を図3に示した。
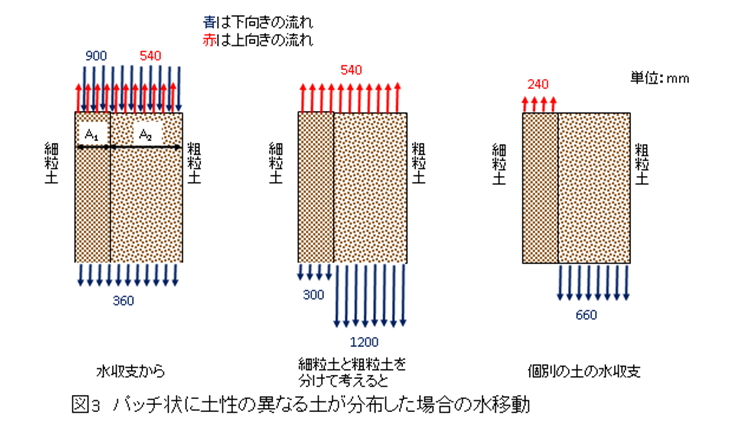
実際のパッチ状の畑はモデルのように単純ではなく,細粒と粗粒の土は平面上にも鉛直状にも存在して複雑である。パッチ状の農地で水稲を栽培すると,水稲栽培期間は湛水により下向きの浸透水は塩を洗い流す。また,水稲根は深さ10cmまでに大半が分布するので,水稲に塩による障害は生じないだろう。しかし,水稲の後に畑作物を栽培しようとすると,細粒土では塩濃度が高すぎて障害を受ける可能性があるというのがモデルから得られる結論である。
塩を伴う水移動には,ここで紹介した塩類集積に加えソーダ質土壌の問題がある。塩類土壌を理解し,改良を目指すならば,イオン交換や沈殿現象の知識が不可欠である。土の物理と化学の両方の知識が必要とされる学問的にも非常に興味深い研究分野である。