温度
温度
温度を測る
温度を測ることは、土壌物理研究の中でも多く行われます。
物理現象のほとんどが温度に影響されるからです。
同時に、温度測定は電気計測の始めでもあり、終わりでもあります。それは、「温度測定」のなかに電気計測の方法や考え方のほとんど大部分が含まれているからです。
私は正確に温度を測ることができたら、電気計測は”卒業”と言えるとさえ思っています。たとえば、1/100 ℃の精度で温度を測るためには、いくつかのバリアーを越える必要があります。
でも、大丈夫。誰にでもできます。
Step by step. 習うより慣れろ!です。
私の口癖ですが、かんたん、かんたん。
さあ、始めましょう!
温度測定の場合、注意しなければならない点
・対象とセンサーとがすばやく同じ温度になること。
・測定したい場所、位置とセンサーの設置場所とができる限り近いこと(できれば同じ場所・位置)。
・測定することで対象に外乱・影響を与えないこと。そのためにはセンサーの熱容量の大きさや、センサーからの発熱に注意すること。
・センサー部分から導線を通じて熱が供給されたり、逆に熱が吸収されないこと。
・センサーに周りからの熱放射を受けないこと。これは気温測定などの場合に注意する。
温度を測る様々な方法がある。
0.標準温度計
1.熱電対
2.ペルチェ素子(サーモモジュール)
3.金属抵抗線
4.サーミスタ
5.放射温度計
0. 標準温度計(棒状水銀温度計の一種)
電気計測そのものではないが、温度精度が校正されている標準温度計は、1本あると温度測定に役に立つ。
0~50℃の範囲で、0.1℃刻みが便利である。ガラスの2重管になっている。1本1万円程度。校正表がついている。ルーペを使うと0.02℃程度は読める。
感熱部分の熱容量が大きいので、温度が安定(平衡)するのに少し時間がかかる。(写真下)

使ったことはないが、白金抵抗体を用いたデジタル標準温度計(たとえば、TL1-R12など)もある。こちらは高価。
1.熱電対
熱電対はゼーベック効果(Seebeck effect)を利用して生じる起電力を利用して測る。
具体的には、下図に示すように、2種類の金属線の2点間に温度差があるとき、起電力が生じることを利用する。別名、温度電池(熱電池)とも言われる。
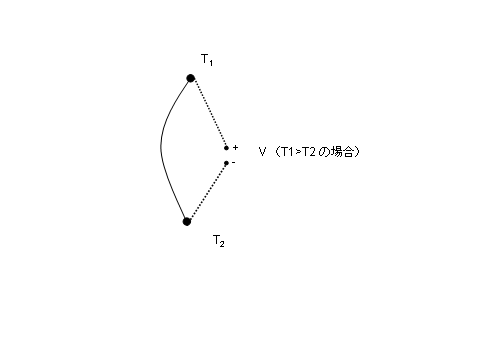
よく使われる銅・コンスタンタン熱電対(Tタイプ)は1℃あたり40μV程度の起電力があるので、0.1℃の精度で測ろうとすると、電圧を4μVまで測る必要がある。
配線の注意
熱電対線は、磁気を横切ると電圧が変化する。これが問題になる場合がある。ためしに、熱電対線を振ってみると、値が大きく振れることがわかる。近くに電動モーターがある場合なども要注意。このような場合、熱電対線を全体にわたってよじると、磁気の影響を小さくできる。
ビニールペアー線はよじれないので、そのままでは無理。必要な場合には線を2本に引き裂いてよじる。
冷接点の準備
起電力の測定は温度差測定なので、基準温度(普通は0℃・・水の氷点)が必要になる。2点間の温度差を測るのなら、一方を基準にすることで測れる。
0℃の状態を作る方法
1気圧で氷と水とが共存する温度(氷点)は0.0℃で温度の基準にすることができる。魔法瓶の中に細かく砕いたフレーク状の氷と水とを入れて、その状態を作る。ここに、熱電対の接点を入れれば、冷接点とすることがでる。
基準点の温度を別の方法(たとえばサーミスタ)で測り、基準点と測定点とから得られた温度差を、基準点の温度に加えれば温度を測ることができる。熱電対で温度が測定できるデータロガーはこの方法を使っている。(端子の温度をサーミスタで測っている。)
温度差だけが必要な場合
冷接点を、温度が安定な状態にして測る。
水の入った瓶を用いる方法、金属のブロックに小さな穴を開けそこに冷接点を入れる方法など(水が使えない高温条件や気圧が低い場合など)工夫次第で様々な基準温度状態が作れる。この場合、注意しなければならないのは次に書く、起電力の温度依存性である。
起電力の温度依存性
熱電対を使う時の注意点は、起電力が温度によって変わることである。理科年表によると、CC熱電対の起電力は、0-10℃で39.1μV/℃、100-110℃で、47.2μV/℃。私は、正確な温度差を必要とするときは、理科年表の起電力を使って温度と起電力の関係をカーブ・フィッティングで多項近似し、この微分値を用いて使用する温度での起電力を得た。
また、装置の起電力は正確な温度計があれば、自分で校正することもできる。
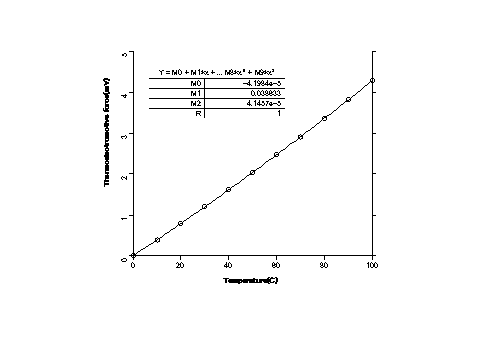
熱電対の種類
熱電対には多くの種類がある。用途によって使い分けることができる。専門書や理科年表に出ているので参考にする。
接点の作り方
熱電対の接点は溶接がいいと本に書かれている場合がある。しかし。溶接は素人の私たちには難しいので、ハンダ付けで十分である。また、ハンダに似た「ろう付け」という方法で接着する方法(たとえば、銀ろう付け)もある。こちらは高温でハンダが融けてしまう場合など、ハンダ付けが利用できない場合に用いる。
熱電対の素線をよじって、ハンダをさっと乗せる。よじる部分は数ミリでOK。長めによじって、あとでニッパーで接点部分を短く切り取るのもいい。
ビニール線で2芯の熱電対で温度を測る場合(地温、水温など)、ハンダ付けした接点部分を2液混合のエポキシ接着剤で被覆するのが便利である。エポキシ樹脂はビニールとも相性がいいので、接点だけでなく全体が防水できる。私はこれを多用した。
熱伝導率のヒートプローブのなかに入れる細い熱電対の接点の被覆には、薄く塗れるペンテルの修正液を使った。被覆した部分が白くなるので、使いやすい(熱伝導率測定用のヒートプローブの作り方については別項で説明する。)
熱電堆(ねつでんたい)
熱電堆を利用して温度差を測ることができる。これは、熱電対を直列に複数使うと(図)、ちょうど電池を直列したのと同じ効果があり、起電力が増幅できる。たとえばCC熱電対を10対(つい)直列にすると、1℃あたりの起電力は400μVになる。
温度差を増幅するのに便利。
私は、双子型恒温壁熱量計を使って土の比熱を測るときに熱電堆を利用した。注意しなければならないのは、10対の熱電対を使う場合には熱電対線が合計で20本にもなり扱いづらいこと、もう1点は、熱がこの線の中を流れて逃げるので、できるだけ細い線を使う必要があること。
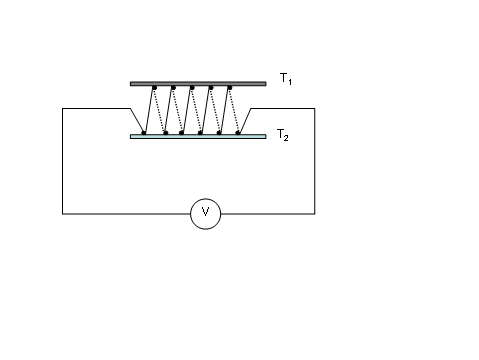
熱電対を使う温度測定の感度は、接点部分の熱容量に依存する。
接点部分を何かで覆えば(たとえば樹脂)それが外界と同じ温度になるまでに時間がかかる。感度を上げるには、接点部分の熱容量を小さくする。
逆に接点部分の熱容量を大きする場合もある。あまり短時間で温度変化が大きい場合、平均化するために意図的に熱容量を大きくする。気温測定などに向いている。
2.ペルチェ素子(サーモモジュール)
ペルチェ効果はゼーベック効果の逆で、熱電対に電気を流すと両接点に温度差が生じる現象である。
車載用の冷温庫はこの原理を応用している。そのために作られた素子がペルチェ素子(サーモモジュール)写真下。

薄い2枚の薄いセラミック製放熱板の中にP型とN型の熱電半導体を下図のように複数個直列に接続したもの。熱電対のところで示した熱電堆と同じ原理である。
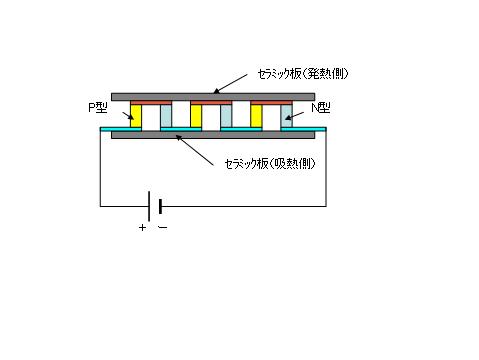
この素子を本来の温度差を作り出す目的でなく、ゼーベック素子として使うと温度差が測定できる。特徴は1℃当たりの起電力が数mVと非常に大きくなることで、正確な温度差が測定できる。
これを利用して、微小な熱量を測定できる熱量計の温度センサーに使われている。
私たちは定常型熱伝導率測定装置に、この素子を使って熱流量測定に利用しました。詳細は定常型熱伝導率測定装置をご覧いただきたい(いずれ書きます)。
3.金属抵抗線
金属の電気抵抗は温度依存性があり、温度が高くなるほど抵抗が大きくなる。絶対零度付近では電気抵抗がゼロになるという超電導現象はよく知られている。
抵抗の温度依存性は金属抵抗の温度係数で表す。
R(T) = R0(1+α(T - T0))
ここで。αは温度係数[1/T]、 温度TおよびT0における抵抗値をそれぞれR(T)、R0とする
抵抗変化を利用して温度測定に用いいることができる。
温度測定に用いられる白金の温度係数は、0.0039/K(20℃)、ニッケルのそれは、0.0067(20℃)である。詳細は専門書に。
温度計数の小さいのは、マンガニン線があり、2.0E-5/K(0.00002/K)程度である。白金の200分の1程度、ニッケルの700分の1程度になる。こちらは、温度変化が小さいので電気抵抗部品に用いられる。
金属線の電気抵抗は、線が細いほど、また長くなるほど大きくなる。
温度測定に用いる金属線は白金の場合、100Ωで、長さ100cm、線径0.17mm程度となる。
100Ωの小型センサーも販売されている。
金属線で温度を測るには、ブリッジ回路が用いられる。
100Ωの場合、1℃で抵抗値が100 x 0.0039=0.39Ω変化する。
5Vの電圧をかけ、抵抗を5kΩにすると、電流は1mA となる。
4.9k+100Ω 5V で電流は 1mA
電圧は
0.39Ω x 1mA=0.39mV
との変化となり、熱電対の約10倍の値すなわち感度が得られる。
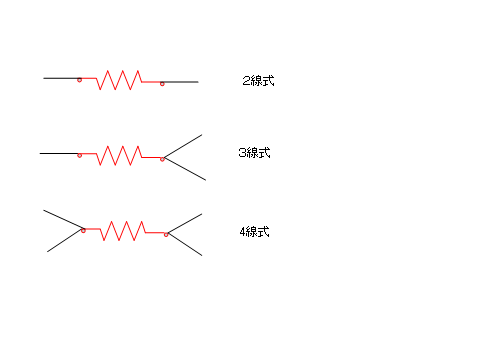
金属温度抵抗体をブリッジ回路につなぐ場合、
2線式、3線式、4線式の3つの方法がある。
2線式は、抵抗体につなぐ導線の抵抗も測定するため、精度は低くなる。
[ 2線式 < 3線式 < 4線式] の順に精度はよくなる。
普通は3線式が多い。
4.サーミスタ
温度変化に対して大きな抵抗値変化を示す抵抗器(セラミック半導体)をサーミスタという。
温度が低くなるほど電気抵抗が大きくなるもの(負の温度特性(NTC・・Negative Temperature Coefficient)をもつもの)が一般的である。金属の電気抵抗とは変化の方向が全く逆になる。
電気抵抗Rは以下であらわされる。
R = R0 exp(B(1/T – 1/T0)
B:サーミスタのB定数(単位は温度) R0は温度T0のときの抵抗値 温度は絶対温度であることに注意。
素子は小さく、抵抗値が大きいため使いやすい(写真)。金属抵抗のような導線抵抗を気にせずに使える。しかし、素子ごとに係数(R0, B)が異なる場合があるので、多数の測定をする場合などは、係数の合った素子を使う必要がある。
T0=25℃(+273.15K)、R0=10kΩ、B=4000の場合
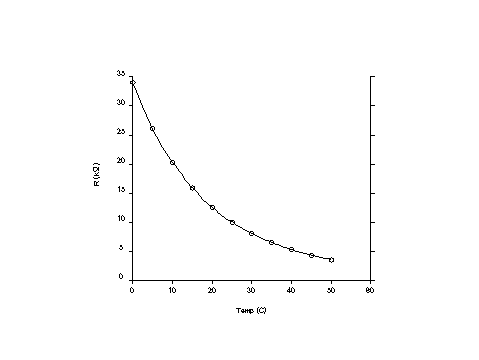
温度(℃) 絶対温度(K) 抵抗値(kΩ)
0 273.15 34.14
5 278.15 26.24
10 283.15 20.35
15 288.15 15.93
20 293.15 12.57
25 298.15 10.00
30 303.15 8.01
35 308.15 6.47
40 313.15 5.26
45 318.15 4.30
上のように指数的に変化するので、実際の回路では直列抵抗と並列抵抗を組み合わせることにより、一定の温度範囲で直線化を行う場合がある。
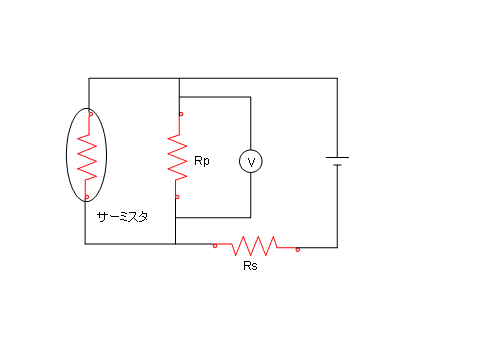
図 温度ーRの直線化回路 RpとRsを選ぶことにより直線化できる
5.放射温度計
全ての物質からその温度に対応した波長の赤外線が放出されている。この赤外線の波長から温度を測定することができる。
地表面の平均的な温度などを知りたい場合には有効な方法である。
6.その他
人の感覚も時に有効な場合がある。0~50℃程度までは、大体の温度はわかる。簡単な温度計としての利用価値は大きい。